
Dr. Saurabh Maiti, PhD
- Associate Professor, Physics
Are you the profile owner?
Sign in to editResearch areas: Collective phenomena and light-matter interaction, Spin-orbit coupled systems, Unconventional superconductors, Engineered 2D lattices
Contact information
Biography
Career
Associate Professor, Concordia University, 2024-present.
Assistant Professor, Concordia University, 2019-2024.
Postdoctoral Scholar, University of Massachusetts, Amherst, 2017-2019.
Postdoctoral Scholar, University of Florida, Gainesville, 2015-2017.
Dirac Fellow, National High Magnetic Field Lab, Tallahassee, 2013-2015.
Education
PhD. Physics, University of Wisconsin, Madison, 2013.
BTech(Honors), Electronics and Electrical Communications Engg., Indian Institute of Technology, Kharagpur, India, 2007.
Teaching activities
Term courses
PHYS 459/636 Solid State Physics/Condensed Matter Physics I
PHYS 468/637 Condensed matter physics II
PHYS 498/609: Advanced Topics in Physics(Introduction to Quantum Field Theory)
PHYS:768/862 Graduate Seminars
Research activities
Collective phenomena in spin-orbit coupled systems
Spin-orbit coupling that breaks parity (Rashba and Dresselhaus type) results in peculiar quantum properties and new kind of chiral-spin waves. Such a coupling typically manifests itself in 2D/quasi 2D systems and also forms the basis of the emerging field of spintronics/magnonics where the focus is to perform the typical “electronics” using the high efficiency and controllability of spin-based systems. We are interested in identifying and studying new kinds of spin-waves that 2D materials can host; and exploring their topological properties. Some systems we are interested in are hetero-structures/quantum wells, multi-layer Graphene and transition metal dichalcogenides(TMDC). We are also interested in knowing how these waves couple to spectroscopic probes.
Correlation effects from spectroscopy
Some of the most exciting systems in modern condensed matter physics are the high-Tc or unconventional superconductors(SC) and itinerant magnets. We study how signatures of these states could be captured via spectroscopic tools. We are especially interested in modelling the response to look for non-trivial changes due to correlations and symmetry-breaking perturbations to the system. We like to look at electronic Raman scattering, THz pump/probe signals, optical absorption, to name a few.
Engineered 2-dimensional lattices
With the advent of 2D materials, there are many exciting directions that have emerged. In particular, special lattices can be designed with geometrically flat bands is interesting as it offers a unique energy landscape to study effects from strong correlations, effects from the quantum geometry and topology. It also offers a playground to study effects of non-Maxwell type gauge-fields (such as Chern-Simons). Finally, a lot of 2D materials have a Dirac basis for the electronic states which get strained upon structure manipulation. This strain can also be treated as a gauge field. We are interested in exploring the interplay amongst all these fields.
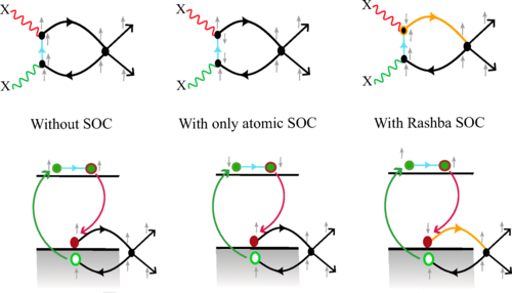
A new mechanism for light-matter coupling via spins!
Image from our work Phys. Rev. B 109, 035160(2024).
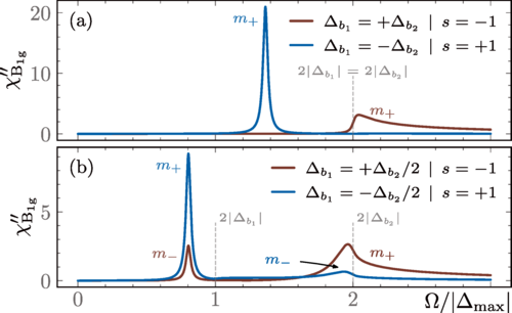
A new selection rule from many-body physics!
From our work Phys. Rev. B 109, 104505 (2024)
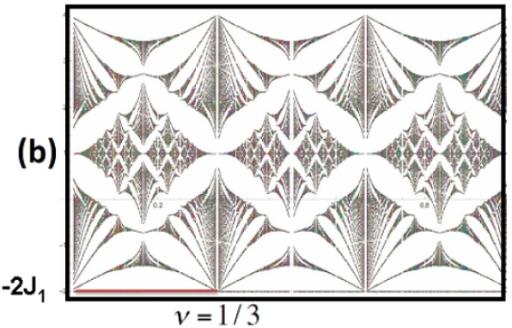
Non-standard Hoffstadter butterfly in Kagome lattice.
Our figure was featured in PRB Kaleidoscope.
Publications
Featured Work and News
Editor's Suggestion (theory) on using light and spins to see Plasmons(2024)
Editor's Suggestion (experiment) on using light and spins to see Plasmons(2024)
Kaleidoscope in PRB (2019).
Altmetric score of over 100! (2017).
Synopsis in Physics (Dec, 2011).
Synopsis in Physics (Jun, 2011).
Publications and citations:
Google Scholar
Selected Publications
Condmat arXiv
Chapters/Books
Superconductivity from repulsive interactions, Saurabh Maiti and Andrey Chubukov,
Chapter 15, Novel Superfluids, Vol. 2, ed. by Karl-Heinz Bennemann and John B. Ketterson, Oxford University Press (2015).
Outreach
Quantum Physics and the everyday world
(2024) Invited to Northwest Missouri State University to speak about relevance of quantum physics to everyday life on the World Quantum Day
Quantum excitement: What particles do, and what we can make them do using quantum physics
(2020)Invited to speak at Dawson College for their experiential learning program.

