HeroSvm 2.1
Introduction
Support Vector Machine (SVM) represents the state-of-the-art classification technique. However, training SVM on a large training set becomes a bottleneck. HeroSvm is a high-performance library for training SVM for classification to solve this problem. It has been implemented based on our proposed method [1][5][22]. In order to facilitate the software portability and maintenance, an object-oriented method has been applied to design the package. Error handling is supported and HeroSvm is exception-safe. HeroSvm is written in C++. In the current version, a dynamic link library in windows or a shared library in linux is provided to train SVM on a large-scale learning problem efficiently for research purpose in PC platform. We expect that HeroSVM can facilitate the training of support vector machine and solve some real-world problems in various engineering fields.
- 40 times faster than HeroSvm 1.0
- Train SVM with thousands of classes
- Support large training set with several million samples
- Provide a complete demo program, which includes SVM training and testing routines
- Only support Pentium 4 and above. HeroSvm 1.0 does not have this limitation.
- Only support RBF, Polynomial and linear kernels. HeroSvm 1.0 supports a user-specified kernel.
- Much faster than the previous training method, especially on a large training set with many classes
- Simple function interface
- Detailed user guide
- Error handling is supported and exception-safe.
- No limitation on the size of the training set and dimension of feature vectors.
- Efficient algorithm to speed up the evaluation of SVM in the testing phase
- Support windows and Linux
- Compared to HeroSvm2.0, the version 2.1 provides a very efficient algorithm to speed up the evaluation of SVM for multi-class classification in the testing phase [29].
- Support Linux
- PC, RAM (at least 256 Megabytes)
- Only single thread is supported
- Feature-based suppport vector machine is applied to three well-known handwritten digit databases and has obtained the-state-of-the-art generalization performance on all four public handwritten character databases, given as follows
| Database | Training set | Testing set |
| CENPARMI (digit) | 4000 | 2000 |
| USPS (digit) | 7291 | 2007 |
| MNIST(digit) | 60,000 | 10,000 |
| NIST database (lowercase characters) | 24,092 | 10,688 |
| Methods | Raw Error rate without rejection (%) |
| Cho's [2] | 3.95 |
| S. W. Lee [3] | 2.20 |
| Local Learning Framework [4] | 1.90 |
| Virtual SVM [5] | 1.30 |
| SVC-rbf [6] | 1.10 |
| Classifiers | Training set | Raw error rate without rejection (%) |
| Nearest-neighbor [7] | USPS+ | 5.9 |
| LeNet1[8] | USPS+ | 5.0 |
| Optimal margin Classifier [9] | USPS | 4.6 |
| SVM [10] | USPS | 4.0 |
| Local Learning [11] | USPS+ | 3.3 |
| Virtual SVM, local kernel [12] | USPS | 3.0 |
| Boosted Neural Nets [13] | USPS+ | 2.6 |
| Tangent Distance [7] | USPS+ | 2.6 |
| Feature-based virtual SVM [5] | USPS | 2.34 |
| Combination of tangent vector and local representation[28] | USPS | 2.0 |
| Virtual SVM [14] | USPS | 3.2 |
| Human error rate [15] | --- | 2.5 |
| Human error rate [16] | --- | 1.51 |
| *Note that training set on USPS+ contains some machine-printed patterns. | ||
| Methods | Raw Error rate without rejection (%) |
| 3-NN [17] | 2.4 |
| LeNet1 [17] | 1.7 |
| 400-300-10 network [17] | 1.6 |
| Polynomial SVM [18] | 1.4 |
| Tangent Distance [17] | 1.1 |
| LeNet4 [17] | 1.1 |
| LeNet5 [17] | 0.9 |
| Virtual polynomial SVM [19] | 0.8 |
| Boosted LeNet4 [17] | 0.7 |
| Virtual SVM with 2pix VSVx [20] | 0.56 |
| SVM on vision-based feature [23] | 0.59 |
| Feature-based SVM [5] | 0.60 |
| PCA-based SVM [5] | 0.60 |
| VSVMa [5] | 0.44 |
| SVC-rbf [6] | 0.42 |
| VSVMb [5][21] | 0.38 |
| Methods | Raw Error rate without rejection (%) |
| GLVQ [4] | 10.17 |
| MQDF [4] | 10.37 |
| 160-100-27 MLP [4] | 8.40 |
| Local Learning Framework [4] | 7.66 |
| Feature-based SVM [5] | 7.44 |
| VSVM | 6.70 |
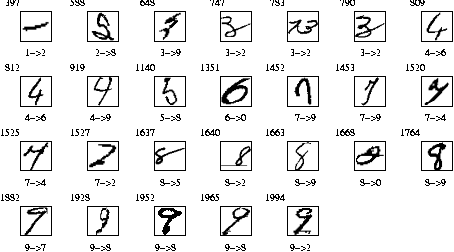
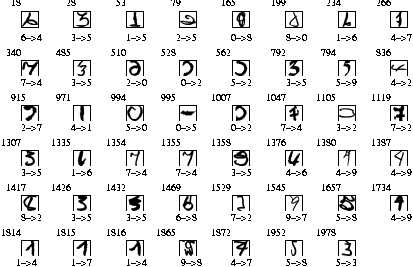
Fig. 1 The 47 errors ( 2.34% error rate) for the USPS test set. The number in the upper-left corner of each image indicates the test sample number. The first digit on the bottom specifies the true label. The second digit on the bottom is the recognized digit label. From the above figure, it can be seen that there are obviously four errors in the original labelling (234, 971, 994, 1978).
Misclassified patterns on the test set of MNIST
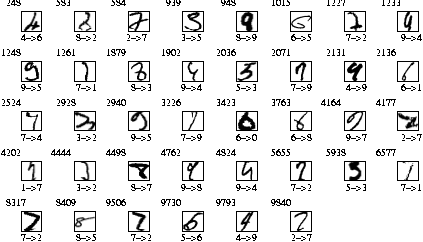
Fig. 2 The 38 errors ( 0.38% error rate) for MNIST test set. The number in the upper-left corner of each image indicates the test example number. The first digit on the bottom specifies the true label. The second digit on the bottom is the recognized digit label.
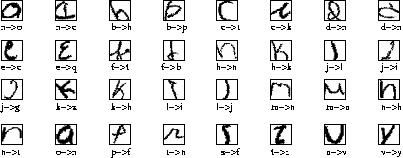
Some misclassified patterns on NIST lowercase character database
In some real world application such as check recognition, the reliability rate is more important than the raw error rate. So it is necessary to evaluate SVM's rejection performance. The reliability is defined by:
Reliability = Recognition rate /(100% - Rejection rate )
Patterns are rejected when the difference between the outputs of the top two classes is smaller than a predefined threshold beta . Experiments aimed at evaluating rejection performance were conducted on MNIST database. The results is shown in the following Table:
Rejection Performances for VSVMa under different beta
| beta | Recognition rate | Substitution rate | Rejection rate | Reliability |
| 1.1 | 96.69% | 0.04% | 3.27% | 99.96% |
| 1.4 | 94.41% | 0.01% | 5.58% | 99.99% |
| 1.7 | 91.51% | 0 | 8.49% | 100% |
| --- | 99.56% | 0.44% | 0 | 99.56% |
Two large handwritten digit database and ETL9B and Hanwang (handwritten Chinese character database) are used to test the performance of HeroSvm2.0. Some important performance measures are listed in the following Table.
Testing platform:
P4 1.7Ghz with 256K L2 (second-level ) cache, 1.5 Gegabytes SDRAM (Single Data Rate Memory).
Operating system: Windows 2000 Professional
| Database | Classes | Training set | Testing set | Feature dimension | Kernel | Total training time (Proposed) | Training time for Keerthi et al.'s SMO | Training time for modified Svmlight-A[24](v5.00) (one-against-others) |
Training time for modified svm-light -B(v5.00) (one-against-one) |
Training time for Modified libsvm-A[25](v2.4) (one-against-others) |
Training time for Modified libsvm-B(v2.4) (one-against-one) |
Testing error rate | Speed-up factor for Keerthi et al's SMO | Speed-up factor for modified Svmlight -A | Speed-up factor for modified svmlight -B | Speed-up factor for Modified Libsvm-A | Speed-up factor for Modified libsvm-B |
| Hanwang(handwritten digit) | 10 | 1321718 | 300000 | 120 | RBF | 0.75 hours | ---- | ------- | 7.63 hours | --------- | 16.21 hours | 0.5% | -------- | --------- | 10.17 | --------- | 21.61 |
| MNIST (A) | 10 | 60000 | 10000 | 576 | RBF | 0.064 hours | 10.4 hours | 1.11 hours | 0.37 hours | 3.04hours | 0.39 hours | 0.6% | 161.38 | 17.22 | 5.74 | 47.17 | 6.09 |
| MNIST(B) | 10 | 60000 | 10000 | 784 | Polynomial | 0.075 hours | 21.44 hours | 2.03 hours | 0.54 hours | 4.52 hours | 0.54 hours | 1.1% | 285.87 | 27.07 | 7.2 | 60.27 | 7.20 |
| ETL9B | 3036 | 485760 | 121440 | 392 | RBF | ------ | ------- | --------- | 1.1% | -------- | --------- | --------- |
|||||
| Hanwang (handwritten Chinese) | 3755 | 2144489 | 542122 | 392 | RBF | 19.28 hours | ------- | ------- | 644 hours | --------- | 3.03% | --------- | --------- | 33.40 | --------- |
||
| RingNorm | 2 | 100,000,000 | 3,000,000 | 20 | RBF | 15.89 hours | 1.24% |
Note: Speed-up factor = training time for one algorithm /training time for the proposed algorithm.
Note that Keerthi et al's improved SMO was implemented by myself by following the pseudo code in the technical report [26].
Note: Modified libsvm-B and svmlight-B use one-against-one method for multi-classes; other methods use one-against-others.
Pre-conditions of performance comparion:
- Dense feature vector which is stored in a contiguous memory address.
- Almost the same size of kernel cache.
- The fixed stopping tolerance.
- The fixed experimental platform.
- The fixed kernel parameter and C.
Post condition:
- After training, the error rate on the testing set must be very close.
| Database | HeroSvm2 IO (read/write file) time | HeroSvm2 Peak (Megabytes) of memory usage | modified SVMlight (v5.00) -A Memory Usage (Megabytes) | Modified Svmlight(v5.00)-B Memory Usage (Megabytes) | Modified LIBSVM-A (v2.4) Memory Usage (Megabytes) | Modified Libsvm-B (v2.4) Memory Usage(Megabytes) |
| MNIST (A) RBF | 5.02 seconds | 384 | 425 | 430 | 460M | 180M |
| MNIST (B) Poly | 7.98 seconds | 427 | 455 | 460 | 485 | 210M |
| Hanwang handwritten digit database | 14.57 seconds | 579 | ---------------- | 840 | -------------------- | 810 M |
| **Note that training time of Svmlight and LIBSVM does not include IO time. | ||||||
The detailed algorithms, which solve the bottle-neck problem of low classification speed in the testing phase, are referred to [21][29]. The proposed algorithm dramatically boosts the classification speed of SVM without sacrificing the accuracy of the original SVM in the testing phase, especially for multi-class classification. The experiments were conducted on the same platform as above.
| Database | Kernel | Dimension of feature vector | Total number of merged Support vectors | Classification speed of the original SVM | Classification speed of the approximated SVM | Speed-up factor |
| MNIST | RBF | 576 | 9739 | 149patterns/second | 16393 patterns/second | 110 |
| Hanwang digit database | RBF | 120 | 41417 | 62patterns/second | 10895 patterns/second | 175 |
If you like to use this software in research or commercial applications, please contact Nicola Nobile, technical manager at CENPARMI.
- User guide
- Header file (SVMTrain.h)
- Distributed package
- User guide
- USPS data
- Header file (SVMTrain.h )
- Distributed package
- MNIST dataset for RBF kernel. Training vector consists of discriminative features (MNIST_576_RBF.zip) (about 100M)
- MNIST dataset for Polynomial kernel. Training vector consists of pixel values. (MNIST_784_POLY.zip) (about 62M).
- ETL9B dataset for RBF kernel. Training vector consists of discriminative features. (soon)
Note: MNIST handwritten digit database is originally built from NIST dataset by LeCun research group at AT&T lab. If you use this dataset in your research, please cite LeCun et al.'s paper [27] to acknowledge their contribution.
[1] J. X. Dong, A. Krzyzak, C. Y. Suen, A fast SVM training algorithm. International workshop on Pattern Recognition with Support Vector Machines. S.-W. Lee and A. Verri (Eds.): Springer Lecture Notes in Computer Science LNCS 2388, pp. 53-67, Niagara Falls, Canada, August 10, 2002.
[2] S.B. Cho and J. H. Kim, ``Combining multiple neural network by fuzzy integral for robust classification," IEEE Trans. Systems, Man and Cybernetics, vol. 25, no. 2, pp. 380--384, 1995
[3] S. W. Lee, ``Multilayer cluster neural network for totally unconstrained handwritten numeral recognition," Neural Networks, vol. 8, no. 5, pp. 783--792, 1995
[4] J. X. Dong, A. Krzyzak. and C. Y. Suen, Local Learning Framework for Handwritten Character Recognition. Engineering Applications of Artificial Intelligence, vol. 15, Issue 2, pp. 151--159, April 2002.
[5] J. X. Dong, A. Krzyzak, and C. Y. Suen, "Fast SVM Training Algorithm with Decomposition on Very Large Datasets," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 27, no. 4, pp. 603--618, April 2005.
[6] Cheng-Lin Liu, Kazuki Nakashima, Hiroshi Sako and Hiromichi Fujisawa, "Handwritten Digit Recognition Using State-of-the-art Techniques,"Proceedings of the eighth International Workshop on Frontiers in Handwriting Recognition, pp. 320--325, Niagara-on-the lake, Canada. August 6--8, 2002
[7] P. Simard, Y. LeCun, and J. Denker, "Tangent prop -- a formalism for specifying selected invariance in an adaptive network," in Advances in Neural Information Processing Systems, J.E. Moody, S.J. Hanson, and R. P. Lippmann, Eds., vol. 4, Morgan Kaufmann, San Mateo, CA, 1993
[8] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R.E. Howard, W. Hubbard, and L.J. Jackel, "Backpropagation applied to handwritten zip code recognition," Neural Computation, vol. 1, pp. 541--551, 1989
[9] B.E. Boser, I.M. Guyon, and V.N. Vapnik, "A training algorithm for optimal margin classifiers," in Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory, D. Haussler, Ed., pp. 144--152, ACM Press, Pittsburg, PA, 1992.
[10] B. Scholkopf, C.J.C. Burges, and V. Vapnik, "Extracting support data for a given task," in Proceedings, First International Conference on Knowledge Discovery and Data Mining, U.M. Fayyad and R. Uthurusamy, Eds., pp. 252--257, AAAI Press, Menlo Park, CA, 1995
[11] L. Bottou and V. Vapnik, "Local Learning algorithm," Neural Computation, Vol. 4, no. 6, pp. 888--901, 1992
[12] B. Scholkopf, Support Vector Learning, Ph.D. thesis, R. Oldenbourg Verlag, Munchen., Technical University of Berlin, 1997
[13] H. Drucker, R. Schapire, and P. Simard, "Boosting performance in neural network," International Journal of Pattern Recognition and Artificial Intelligence, vol. 7, no. 4, pp. 705--719, 1993
[14] B. Scholkopf, C.J.C. Burges, and V. Vapnik, "Incorporating invariances in support vector learning machines," in Artificial Neural Network-ICANN'96, C. von der malsburg, W. von Seelen, J.C. Vorbruggen, and B. Sendhoff, Eds., vol. 1112, pp. 47--52, Springer Lecture notes in Computer Science, Berlin, 1996.
[15] J. Bromley and E. Sackinger, "Neural-network and k-nearest-neighbor classifiers," Tech. Rep. 11359--910819-16TM, AT&T, 1991
[16] Jian-xiong Dong, Statistical Results of Human Performance on USPS database. Report. CENPARMI, Concordia University, October 2001. ( Labelling date file of four subjects. USPS images for test set.)
[17] Y. LeCun, L.D. Jackel, L. Bottou, J.S. Denker, H. Drucker, I. Guyon, U.A. Muller, E. Sackinger, P. Simard, and V.N. Vapnik, "Comparison of learning algorithms for handwritten digit recognition," in Proc. Int'l Conf. Artificial Neural Networks, pp. 53--60, Paris, 1995
[18] C.J.C. Burges and B. Scholkopf, "Improving the accuracy and speed of support vector learning machines," in Advances in Neural Information Processing Systems, M. Mozer, M. Jordan, and T. Petsche, Eds., vol. 9, pp. 375--381, MIT Press, Cambridge, MA, 1997.
[19] B. Scholkopf, P. Simard, and V. Vapnik, "Prior knowledge in support vector kernels," in Advances in Neural Information Processing Systems, M. Jordan, M. Kearns, and S. Solla, Eds., vol. 10, pp. 640--646, MIT Press, Cambridge, MA, 1998.
[20] D. DeCoste and B. Scholkopf, "Training invariant support vector machines," Machine Learning, vol. 46,no. 1-3, pp. 161--190, 2002
[21] J. X. Dong, Speed and accuracy: large-scale machine learning algorithms and their applications. Ph.D. thesis. Department of Computer Science, Concordia University, Montreal, 2003
[22] J. X. Dong, C. Y. Suen and A. Krzyzak, A fast parallel optimization for training support vector machine. Technical Report, CENPARMI, Concordia University, October, 2002.
[23] L.N. Teow and K.F. Loe, Robust vision-based features and classification schemes for off-line handwritten digit recognition. Pattern Recognition, vol. 35, pp. 2355--2364, 2002.
[24] T. Joachims, Making large-scale SVM Learning Practical. Advances in Kernel Methods-Support Vector Learning, B.Scholkopf and C. Burges and A. Smola (eds.), MIT Press, 1999. Svm-light is available from http://svmlight.joachims.org/
[25] Chih-Chung Chang and Chih-Jen Lin, Training nu-Support Vector Classifiers Theory and Algorithms. Neural Computation, vol. 13, pp. 1443--1471, 2001. Libsvm is available from http://www.csie.ntu.edu.tw/~cjlin/libsvm/
[26] S.S. Keerthi, S.K. Shevade, C. Bhattacharyya and K.R.K. Murthy, Improvements to Platt's SMO algorithm for SVM classifier design, Technical Report CD-99-14, Control Division, Dept. of Mechanical Engineering, National University of Singapore, 1999. see electronic version from the web: http://guppy.mpe.nus.edu.sg/~mpessk/publications.shtml
[27] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, Gradient-based learning applied to document recognition. Proceedings of the IEEE, vol. 86, No. 11, pp. 2278--2324, November 1998
[28] D. Keysers, R. Paredes, H. Ney, and E. Vidal, Combination of Tangent Vectors and Local Representation for Handwritten Digit Recognition. In SPR2002, International Workshop on Statistical Pattern Recognition, Windsor, Ontario, Canada, Volume LNCS 2396 of Lecture Notes in Computer Science, Springer-Vertag, pp. 538--547, Aug. 2002.
[29] J.X. Dong, A. Krzyzak and C.Y. Suen, "Algorithms of Fast Evaluations based on Subspace Projection," Proceedings of IEEE International Joint Conference on Neural Network (IJCNN'05), Montreal, Quebec, July 31-August 4, 2005.


